Advocacy
Dojo (HowTo)
Reference
Markets
Museum
News
Other
1
![]()
Myths
Press
General
Hack
Hardware
Interface
Software
Standards
People
Forensics
Web
CodeNames
Easter Eggs
History
Innovation
Sightings
Opinion
Martial Arts
ITIL
Thought

![]()
|
|
|
How
does Compression work
|
|
|
Many people don't understand compression -- how do you make something smaller? In some ways you don't -- you just encode the data in a more efficient way. This article will explain a few basic types and concepts about data storage and compression. These concepts are far simpler than people realize -- it's just the implementation details can be a pain.
Basically, compression on computers is achieved by looking for commonality (in shape or pattern), and then saving the description of that shape or pattern (using tables or mathematical algorithms) instead of saving the whole image itself. If you don't get it, read on, and it may become more clear.
Shape Compression
Shape compression is usually used for images (but can apply to sound and the wave forms, and so on). Data is seldom random: there is some pattern if you look for it. So we can use that; instead of saving an image, you look for commonality in the image, and create a table of those common elements. Then you just save references (index into the table) of those common elements in a way such that the image can be recreated from its parts.
Characters
One simple form of shape compression would be to look at text. Lets look at a bitmap (binary pattern) for a font (typeface). If you look at an 'A', let's say it takes 8 x 8 dots to represent this character as a bitmap (image). A byte is 8 bits (each of which represent one of our dots), so it takes 8 characters (bytes) to represent an 'A'. (I also did a simple 'B', and 'C', as well).

This sample font is probably a little smaller (less detailed) than the body of text for this article (assuming you are reading it on screen).
Let's say you wanted to save a few pages of text. If you saved the image (bitmap) for all those characters, it would be inefficient. Each page of text is made of about 2,000 characters, and each character is made up of 8 x 8 pixels (x colors) and so on (2). So it would probably take 2000 characters x 8 bytes x how many pages (lets say 3 pages) -- or at least 48K (Kilobytes) to save a few pages of text (as images) -- and that's not counting blank spaces, and so on.
(2) 8 x 8 pixels x 1 color assumes a very small and boring font. A larger font like a title or even the font in the Mac's menu bar is usually more like 14 x 9 -- or about twice as large (in storage). Color information requires far more storage as well.
Instead of saving the page as an image (or a bunch of images), what if we look for the commonality in shapes. We know that an 'A' will look like all other 'A's. So for each character we create an image of that character, and add it to a table (assign each character a unique value). Then instead of saving the image for each character, we save its position in our character table (called a look-up table, 'cause it is where we look things up). When you want to display the image, you just look-up the graphic in the table, using its unique value (index).
One byte can encode 256 different characters (more than we will ever need). So for each byte of data, we can save a character -- instead of having to save all the graphics for each character. This is at least 8 times as efficient for small fonts (8:1 compression). But for larger fonts it can be dozens or hundreds of times as efficient. (3)
(3) You just learned how text is saved on computers. Most Computers use a standard look-up table for those characters, called ASCII. There is a new international format (called Unicode) that allows computers to encode any character in the world (including all those thousands of Chinese and Japanese characters).
This is an efficient form of shape compression. Since our characters are standardized, it is pretty easy to do. We just looked for common shapes (each letter), and figured out a way to describe those shapes (using a table), and then we only remembered an index to table (instead of remembering the shape itself). This compression works great as long as what is being encoded is a standard shape. It gets trickier, or impossible, if it is not.
Illustration (Drawing)
Images themselves are often called "raw data", and can take a lot of space. These are also called Pictures (Picts), Icons, bitmaps, pixmaps, and so on. Lets look at the following image.
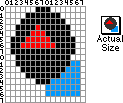
Note: I have the image zoomed in (so we can see the data), and the image in its actual size is to the right of the zoomed image.
If we were to save that as an image, it is 16 pixels (dots) wide, by 16 dots high. This is about the same size as the mouse cursor, or a small icon. Lets assume that we can draw each dot with up to 256 colors -- each byte can represent one of 256 values (Colors). So to encode that image would require 1 byte (pixel color) x 16 pixels (height) x 16 pixels (width), or 256 bytes total to encode that small image.
What if we encoded the data as the shapes themselves? We could save a simple set of tables that would have information about each shape including:
- Which shape it is from a list of 4 shapes (circle, square, triangle and diamond) -- that would require 2 bits.
- We are using 4 colors (black, white, red and blue) -- that would require 2 bits.
- We also want to have to encode the upper-left and
lower-right position for each shape (that encodes size
and position at once) -- that requires 4 bits for each
value (X, Y and X, Y), or 16 bits total.
This makes a total of 20 bits (2 1/2 bytes) for each shape.
Using our shape tables we could draw that same picture with 3 shapes.
- A blue square at position (10,11) to (16,16).
- Then a black circle from (1,0) to (15,14).
- And a red triangle from (3,3) to (11,6).

So it took us just 60 bits, or less than 8 bytes, to encode the same image using illustration or drawing techniques (shape encoding) -- as compared to 256 bytes to encode the raw data. So drawing (in this case) was 32 times more efficient (32:1 compression). But this is only the beginning.
Lets make the image 16 times larger (256 x 256 pixels). It would take 64K (Kilobytes) to encode the raw image, while it would only take about 14 Bytes to encode the drawing -- or better than 4,000:1 compression. So you can see that "drawing" or "illustration" is a far more effective way to encode data than bitmaps (or raw data). Of course the trick to drawing is to have enough shapes, colors and other variants, that the drawing data is useful and can display a variety of pictures (4).
(4) Modern drawing packages can deal with pens of varying widths, many colors, patterns, transforms, curves and complex shapes. So you can imagine that you can do a lot by describing the data as the shapes (drawings).Illustrator, MacDraw, CAD packages and other drawing or illustration programs, encode data as "drawings" (shapes).
Photoshop, MacPaint, and other painting programs, save their data as "paintings" or images -- and take far more space.
The point is that shapes are a far more efficient way of encoding data than images (raw data). But this only works if you can break a problem (image) down into discrete shapes. There are many images that don't fit well into that category. Also, because of the complexity of some drawings, it is very hard to break things down well after the fact. So drawing programs encode data efficiently, but the data has to be created with them in the first place. So there has to be other forms of compression (for image data).
Patterns
When you can't compress data at the source (by describing the data by its parts or common elements), then you have to look for patterns in the data itself. This is usually not quite as efficient, but because of the details of many images, this is how most "pictures" have to be compressed.
Lets do a basic form of pattern compression.
RLE (Run Length Encoding)
Lets encode the following sample:
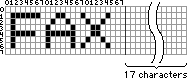
Assuming this image is about 20 characters in size (with only letters in the first few positions). As text it would only take 3 characters (bytes) to encode (one for each letter F-A-X) -- but that only works if we know the font (know what the characters look like) before hand. If we don't know what the font looks like, then we have to go back to encoding the whole thing as an image. As a graphic it would take about 240 bytes to encode the image (1 bit for each pixel). That isn't very efficient. What if instead of encoding the commonality of shapes (characters), we encode based on commonality of the data pattern?
If we look for the commonality in the pattern and we notice there is a lot of white. Lets scan the image pixel by pixel in the same way we read a page of text (from upper left - traveling horizontally until the end of the line, then back to the start of the next line and across, until we get to the bottom right). Notice that there are long runs of white (before you bump into a black pixel). Let's use that.
Instead of encoding just the image as data, lets steal the high bit of a byte, and use that to define if the other 7 bits are going to be data, or a "run" of white (how many bits of white, up to 127+7, should follow).

Encoding the image data is like going "000000000000000000000000...001" in binary. But our compression technique is like saying, "there are 127 - '0's", then a 1. This is a far more efficient way of expressing the data.
At the start of our "run" we notice the first line is white. So we encode a byte with the high bit off (is white), and a run of white for 134 pixels. Then we need another byte (run) to do the same for the remaining 27 more pixels (to get to the start of the black pixel). The next three bytes are encoded as data (image). This is encoded a little less efficient, since we only have 7 bits per byte to use (since we use the high bit for whether it is a white run or not). So the data encodes about 13% less efficient for these bytes, but this is more than made up for by the added efficiency for white runs. So using our encoding, it took only 2 bytes to encode what took 20 bytes as an image -- so our way was 10 times more efficient. The longer the "runs" of white (uninterrupted white), the better the efficiency of our encoding (compression).
This whole technique is called, "Run Length Encoding" or RLE, since we are looking for "runs" (streams) of the same pattern. We could also get fancy and figure out how to encode runs of other patterns as well (like black or alternating bits, and so on), but you should get the idea.
By the way, this is basically how a fax machine works.
More Text
Of course, RLE can also be used to compress text, if the text you were encoding had long "runs" of a particular character. Otherwise there would be no real gains (and potential loss) in efficiency.
There are other ways to compress text as well.
Huffman
The most popular form of compression of text is Huffman encoding. Basically, the concept is still to look for more commonly used characters, and encode them using the fewest bits. The sacrifice is that infrequently used characters will take more bits to encode. But if you figure out (predict) the frequency well, you can get pretty good savings (2:1). On large amounts of text, that can be a lot of space.
The way variable size encoding works is to build a tree with many branches. The end of each branch contains a letter, and the shorter the branch, the smaller it is to encode. Here is a sample tree for the Alphabet:
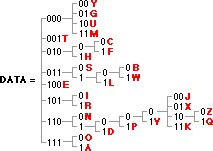
So an 'e' or a 't' (very common letters), take only three bits. The next level, takes 4 or 5, and you just keep adding the bits up, until you are using 10 bits for 'z' or 'q'.
This concept (common = smaller, complex = larger) goes back so far in history, that I wouldn't even want to guess where it started. But a few thousands years ago Chinese (and Western) writing used some of the same concepts. Many of the most common characters are the simplest to write (fewest strokes). They get simplified because people get tired of writing the complex characters all the time -so they "compress" their writing strokes. Another form of this concept might be using morse code. The most common letter in english is the 'e'. So in morse, it is the quickest to send ("dit"). While an uncommonly used letter like 'q' is longer to send (da da dit da).
Lempel/Ziv
If you can variably encode (size), based on character commonality (frequency of occurrence), then when sending text you should be able to compress commonly used words as well. You just have to build tables of hundreds of common (but larger) words, and then send indexes into that table. (Not dissimilar to the Huffman Tree). These indexes are usually built dynamically, by looking into the data itself, then creating the table based on THAT text. Obviously, the fewer the repeats in the document, the less effective the compression.
Several variants of the L/Z algorithms have been pattented, and they demand royalty fees to use. This caused much of the stir over Compuserve's GIF (Graphics Interchange Format) a few years back. Programmers were not thrilled to learn they were going to have to start paying royalties.
Eventhough Huffman and L/Z are usually used to compress text, they same concepts can be applied to other structures like Graphics, Sounds or compound structures.
Conclusion
So there are many kinds of compression techniques. Some other ones not mentioned for graphics include GIF (Compuserve's Graphics Interchange Format), JPEG (Joint Picture Expert Group), MPEG (Motion Picture Expert Group), Fractal based compression (using complex repeating algorithms), and many more. For sound there is AIFF, WAV. Apple's Media Format, QuickTime, has many different file formats and type of compression it supports. And so on. I may go and explain how each of those works in a later article -- I figure this is enough to digest for now.
Remember, all the compression techniques are doing the same basic thing -- they are finding common elements, and encoding the file in a smaller form by only having to save those common elements once.
|
Created: 04/11/98
Updated: 01/22/99